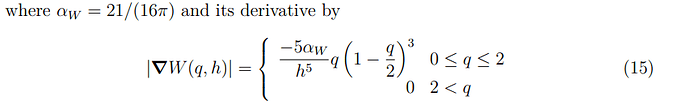Hello!
So I was reading through the Theory Guide for GPUSPH, and I stumbled across this bit;
And what I noticed is that the absolute value of the gradient is used. In theory the gradient of the kernel is anti-symmetric, so particles placed equally distanced on opposite sides, would contribute with opposite signs - of course this will not happen in equation 15, since it only focuses on the normalized distance, q.
I think my confusion might stem from the fact, that I have usually seen the gradient defined as this;
Where the nominator would return a vector with three values, indicating xi - xj, yi - yj and zi - zj etc. In this case, two particles placed on opposite sides, would get a different sign, so the gradient values would be anti-symmetric.
I am probably misunderstanding something along the way, just thought I might ask here, since this is the first time I have seen that the absolute value of the gradient is used.
Hope someone can clear my confusion, kind regards
It’s been a while since I’ve looked over the theory documentation, but isn’t that simply the norm of the gradient? The direction is then given by the inter-particle versor, giving the anti-symmetry. Although I guess it could be explained better …
Actually, I just stumbled upon the following expression later down in the theory document;
This gives me the interpretation that it has to be the absolute value of the gradient. I do not believe it to be a norm of the gradient, since the gradient as expressed here, will only always return a scalar value;
Of course |r_ab| is then the norm, i.e. euclidean distance between particles, so the sign change can only come from “r_ab = r_a - r_b”, but then I would not understand why it is important to use the absolute value of the gradient.
Kind regards
Actually think I just got it. If what I have sketched here is correct;
Then one has to use the absolute value, since the particle on the right, will not be negative then. Still kind of weird for me, but I guess it is a consequence for saying r_i - r_j consistently. Atleast it explains the absolute value now.
EDIT: graph from https://www.sciencedirect.com/science/article/pii/S0307904X13007920
Kind regards